WebGL Fire Shader Based on Fractal Brownian Motion

This is a followup to my previous post on building a shader based on Xflame. I won’t be covering much of the details of building it since they’ll be similar.

You can see the shader in action here. Feel free to pop it open and inspect the code as we go.

There are two primary pieces worth talking about in this one: the noise source and the Fractal Brownian Motion algorithm. As always, The Book of Shaders does a much better job of deep-diving on these topics than I intend to, so if you start to feel lost, I’ll provide links that you can read up on and come back.

I like this approach (and find it surprising) because it’s not recursive on previous frames. Instead, it walks a “fractal-ish” space of intensities that happen to look fire enough to work without having (as far as I can tell) real properties that match it to the way fire behaves physically. The effect is a bit more bonfire than campfire, but I’m suprised at how well it works!

Randomness and noise

In the Xflame shader demo, I talked a bit about randomness and how it’s pretty simple to get something random enough for a graphics application (we’re not trying to do online banking, we’re trying to fool eyeballs). I went ahead and used the same random data source, slightly tweaked to take two arguments.

    <script id="fragment-shader" type="notjs">
      precision mediump float;

      uniform float u_seed;
      uniform vec2 u_screenSize;
      uniform float u_timeSeconds;
      uniform float u_flowRate;

      // Get a pseudorandom value between 0 and 1 from a seed and a lookup
      // See https://thebookofshaders.com/10/
      float prand(in vec2 lookup) {
        return fract(sin((lookup.x * (lookup.y - 5000.)) * u_seed)* 10000.0);
      }

This is a little squirrely, so let’s dig in. First, at the top: our uniform input for random seed is here again. We also have a screenSize 2D vector to make it easy to compute the scale from fragment position coords to a “percentage across screen” value. Fragment coords are (to handwave the details of the spec) in screen pixels, so we just pass the canvas width and height there. The flowRate is a convenient number to control how fast the fire moves up the screen; higher flow rates are faster.

Our random number source returns, only this time, it’s taking two input values and blending them with x * (y + 5000). Why does that work? Our goal here is to, as much as possible, map a 2D numerical space to a 1D space. Ideally, we’d want to do this perfectly, but that’s not really feasible; there is a technical proof that there is no continuous injection from 2D-real numbers to 1D-real numbers (you can get close with things like Hilbert curves, but that’s not really necessary). But we’re not seeking perfection; we’re just trying to fool the eye. As long as our inputs don’t have any obvious patterns mapping them to our outputs across small variances, we’re fine.

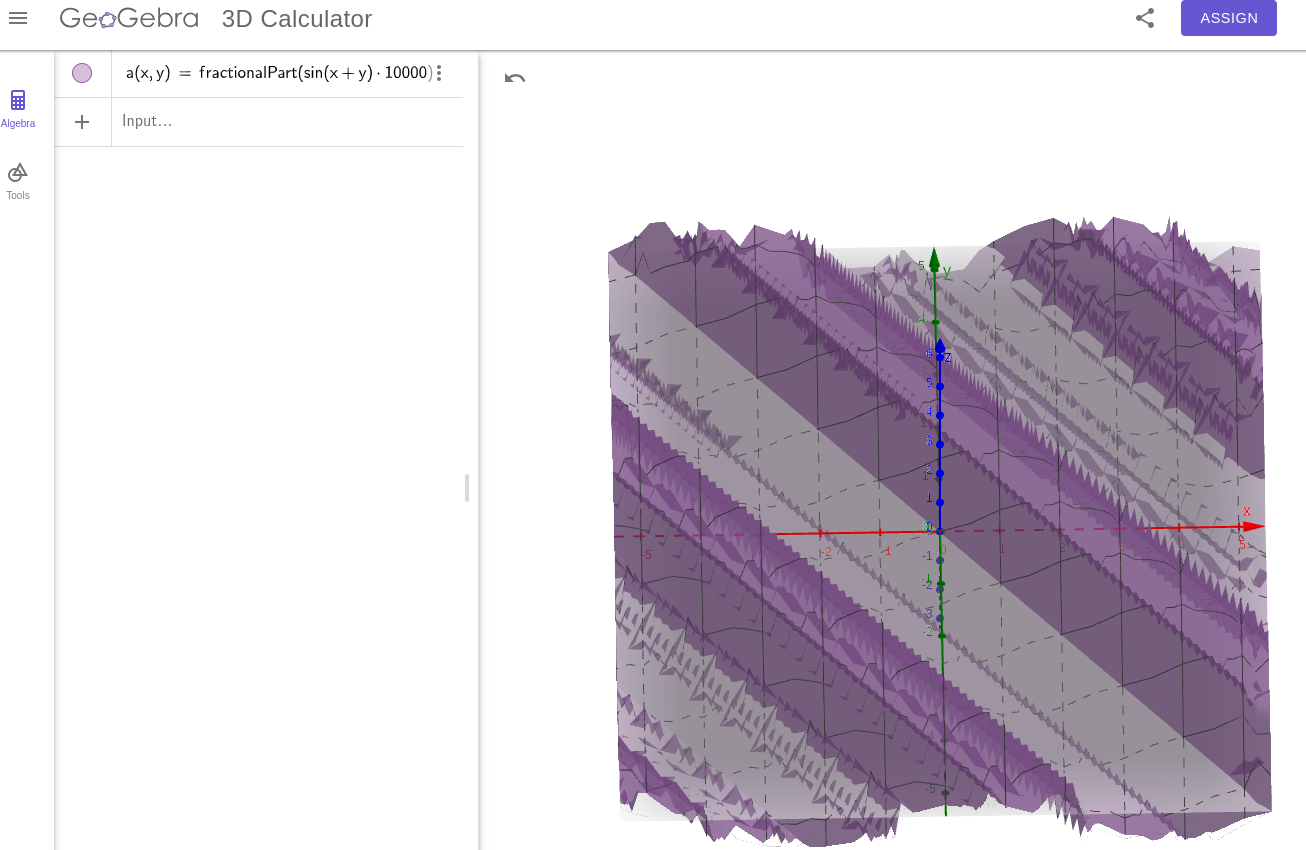
We can try just blending the two inputs: fract(sin(x + y) * 10000.0). Let’s look at that output with the GeoGebra 3D calculator.

Hm, not good. Some obvious patterning in the result. Let’s sanity check that by mapping the values of that function directly to the screen across values from (0,0) to (1,1):

The problem is that there are a lot of values of x and y that map to the same output (x=3 and y=2, x=1 and y=4… Anything on a diagonal line, basically). So we end up with some obvious pattern in our noise. We want to find a way to blend the inputs where adjacent pixes are unlikely to give the same output value.

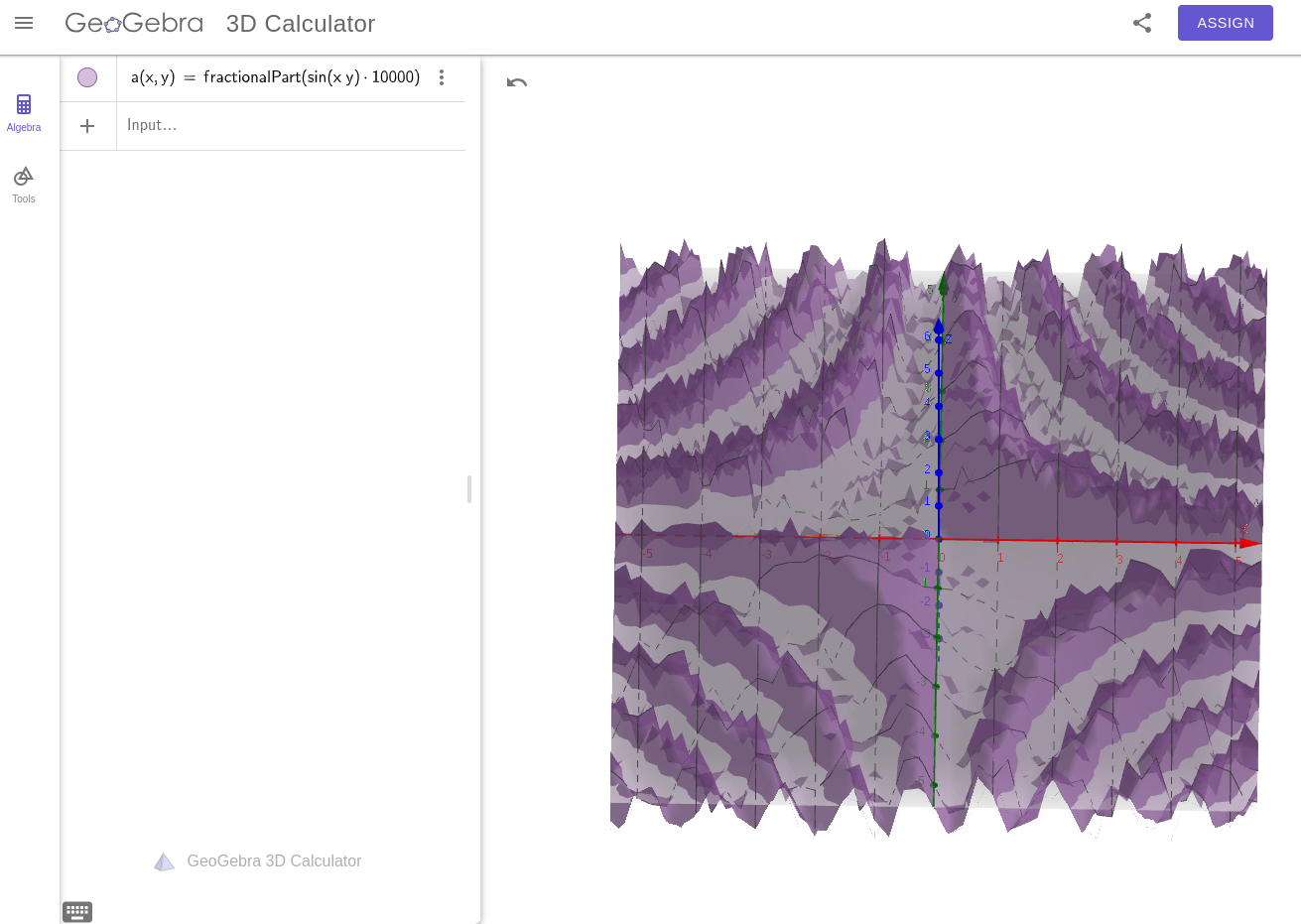
Turns out, multiplying them together gives us some nice curves:

That’s obviously patterned near the origin, but it looks like the fringes are doing something interesting… What if we move away from the origin?

Now we’re cooking. In practice, patterns will emerge if you stare at the noise scrolling vertically, but they don’t stick around long and, more importantly, that’s fine for our problem domain… Naturally burning fire on something like a log has a tendency to occasionally sputter or flare as the fire finds less and more flammable material in the wood, so the occasional development of “macro patterns” fed by non-noisy noise is kind of alright!

The last constant term added to Y is to offset away from the origin so the first immediate pattern in the noise isn’t apparent.

There are other approaches one can take to solving this issue: one can find a lot of hash functions around the web operating on either integer or float inputs. This is not a bad approach to go from two coordinates to a space of values that should be very far apart when the coordinates change slightly, and that’s the goal.

Now that we’ve got a good-enough source of randomness, we can turn it into some nicely smoothed out noise. There are a couple of algorithms here, but it turns out that for our next step, one of the simpler ones works: value noise. Value noise is pretty dead-simple:

• Divide the world into a grid
• At each grid coordinate, pick a random number
• For anything between the grid coordinates, do a linear interpolation of the four random numbers at the corners

You end up with a sort of fuzzy checkerboard (see here, left-hand side). There are other, more smooth and natural noise algorithms (for more information, look into “Perlin noise”), but this turns out good enough.

Here’s how we can get some.

      float noise(vec2 x) {
        // Value noise function. This gives us noise that smoothly interpolates between values in a grid.
        // See https://www.shadertoy.com/view/lsf3WH for example.
        vec2 i = floor(x);
        vec2 f = fract(x);

        // Do a smooth interpolation from [0,1) into a hermite spline on the inputs [0,1)
        vec2 u = smoothstep(vec2(0,0), vec2(1., 1.), f);

        // Four random values for the four corners of our grid square.
        float ll = prand(i);
        float lr = prand(i + vec2(1.,0));
        float ul = prand(i + vec2(0,1.));
        float ur = prand(i + vec2(1., 1.));

        // Interpolate the values of those four points.
        return mix(
          mix(ll, lr, u.x),
          mix(ul, ur, u.x),
          u.y);
      }

And here’s what it looks like if we dump it right to the screen.

Using that as a source, we now have a sort of… Ghost generator? Let’s turn that into fire.

Fractal Brownian Motion feels like cheating

I’m kind of in love with how simple and effective Fractal Brownian Motion (aka Fractional Brownian Motion, the literature disagrees on the name) is. It’s not a hard algorithm at all, but it works amazingly well.

The Book of Shaders has a great write-up on it, but the core idea is simple: lots of stuff in the real world has variation at both low and high frequency. You want to express both. So what you do is:

1. Take a source of noise. Get a noise value.
2. Take the same source of noise. Multiply the input value by some L > 1 and multiply the output by some constant A < 1. Add the new noise to your existing value.
3. Repeat 2 until you get bored, each time scaling L and A by the number of repetitions (repetition 2 is 2L and 2A, repetition 3 is 3L and 3A, etc.).
4. Return all the accumulated values.

The input scaling is akin to frequency and the output scaling is akin to amplitude; in essence, you’re taking a noise source and overlaying on it multiple additional, quieter sources of ever-higher-frequency noise. This is sort of like how vibrating strings in a musical instrucment work: they vibrate at a fundamental frequency but they also vibrate at octaves with ever-lower power at the same time.

Here’s the code.

      float fbm(in vec2 pos) {
        float value = 0.;

        float amplitude = 1.;

        for (int i = 0; i < 4; i++) {
          value += amplitude * noise(pos);
          pos *= 2.0;
          amplitude *= 0.5;
        }

        return value;
      }

The end result looks not bad for a fire base! Cranking up the number of repetitions (“octaves” in the literature) adds more and more high-frequency noise so makes the fire look more “crackly.”

To finish it up, we’ll add just a bit of special sauce:

• Our noise equation tends towards zero at x=0. We add an offset to x in prand to move away from there.
• Instead of looping from (0,0) to (1,1), we loop from (0,0) to (10,2) in our coordinates. That grabs us 20 grid cells, which makes the fire look more granular and gives us more variety in the effect.
• To get a nice flame color, we scale the intensity output by 2.5 and then multiply the whole thing by a nice reddish-orange.
• To make the flames climb, we add time as a uniform u_timeSeconds and translate our function by (-time * flow_rate). This causes us to continuously “walk down” the fractal, which makes it seem to flow up.
• The result of all of this is a wall of fire. To turn it into a roaring fireplace, we add one more bit of scaling, diminishing the intensity the further up the screen we are.

Here’s the last bit of the fragment shader.

      void main() {
         vec2 scaledCoord = gl_FragCoord.xy / u_screenSize;

         // To get some interesting fire variance, we scale the
         // input coordinates to get more grid cells
         vec2 fbmCoord = scaledCoord * vec2(10., 2.);

         fbmCoord += vec2(0, -u_timeSeconds * u_flowRate);

         // fbm(coord) gives us an intensity value from the FBM algorithm. Scale that
         // by how far up the screen we are to fade the fire out nicely and amplify the whole thing
         // by 2.5 to give it a nice bloomy glow.
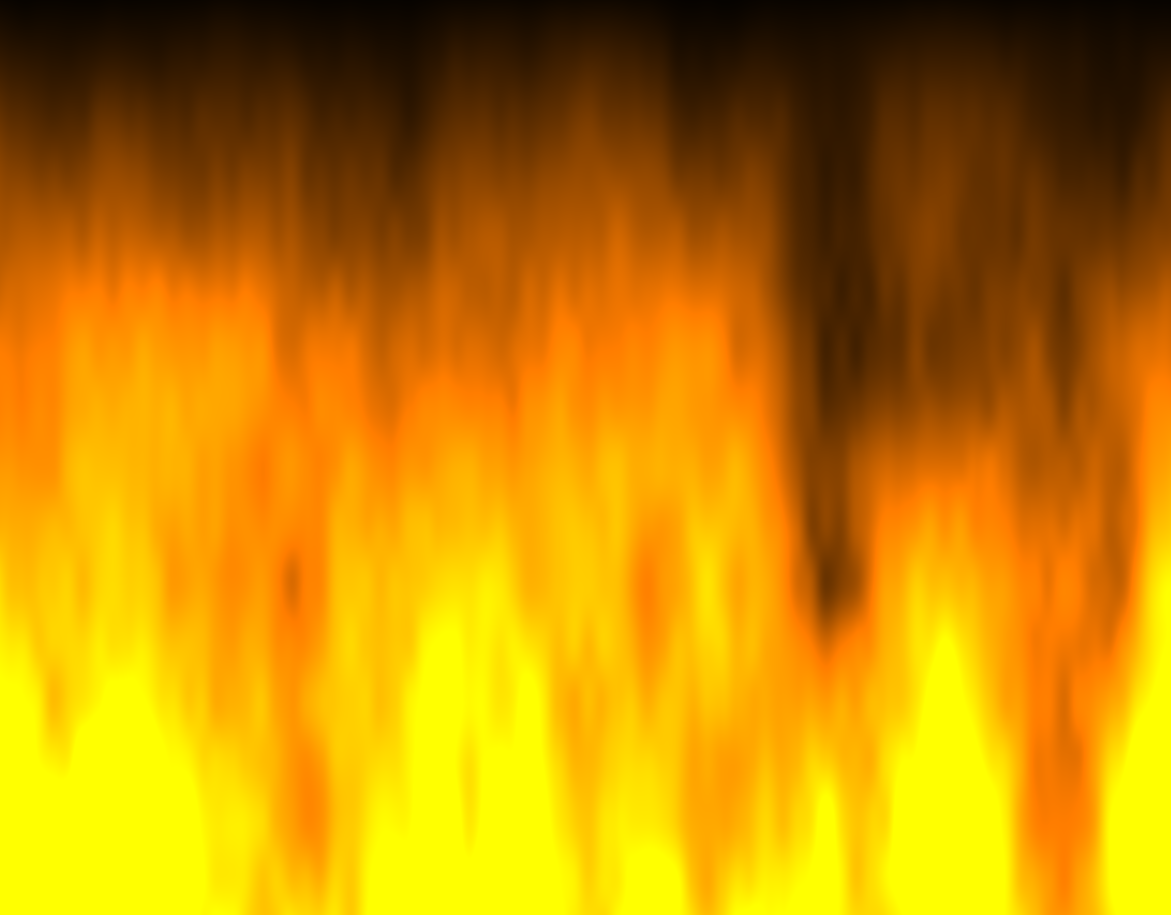
         vec3 color = fbm(fbmCoord) * 2.5 * (1.0 - scaledCoord.y) * vec3(0.9765, 0.4784, 0.);

         gl_FragColor = vec4(color, 1.0);
      }

The end result is pretty nice!

Final thoughts

I find fractal algorithms fascinating because they can describe an arbitrarily-large space that feels at the same time chaotic and connected. This is the same math, roughly speaking, that lets Minecraft churn out a limited-only-by-floating-point-accuracy infinite world where every new chunk sensibly connects to the previous one. And the fact that the equation is closed-form means we get to ignore all the hassle of buffering past state.

There are a few more tweaks I could put on this (I may explore replacing the linear intensity-diminishment as the fire rises with a set of stacked sinewaves regulating the intensity of diminishment so the top of the fire bobs up and down in space more). But I think it’s basically where I want it right now!